에라토스테네스의 체
in Math on Algorithm
소수를 판단하는 알고리즘인 에라토스테네스의 체에 관하여 알아보자.
에라토스테네스의 체
- 수학에서 소수(Prime Number)를 가장 빠르게 식별하는 알고리즘이다.
- *소수 : 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수
- 특정 숫자의 배수는 소수가 아니다는 개념으로 부터 생성되었다.
- 1보다 큰 자연수(즉, 2 ~ $n$ 까지)의 집합에서 특정 수의 배수들을 모두 제거한 뒤에 제거되지 않은 숫자를 소수라고 판단하는 러프한 방식의 알고리즘이다 (이때 특정 수인 자기 자신은 지우지 않는다).
- 넓은 숫자의 범위에서 이 알고리즘을 손으로 수행하면 오랜 시간이 걸리겠지만, 프로그래밍에서는 상당히 효과적이다.
How to?
2 ~ 120까지의 연속적인 숫자 집합에서 소수를 식별하기 위해
에라토스테네스의 체 알고리즘을 적용해보자.
- 2부터 120사이의 숫자를 모두 나열한다.
- 2의 배수(특정 수의 배수)를 반복해서 모두 지운다. (이때 특정 수인 2 자기 자신은 제외한다.)
- 남아있는 수 중 3의 배수(특정 수의 배수)를 반복해서 모두 지운다. (이때 특정 수인 3 자기 자신은 제외한다.)
- 4의 경우 2의 배수를 지울 때 지워졌으므로, 남아있는 수 중 5의 배수(특정 수의 배수)를 반복해서 모두 지운다. (이때 특정 수인 5 자기 자신은 제외한다.)
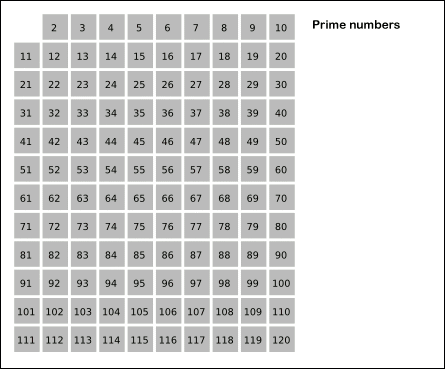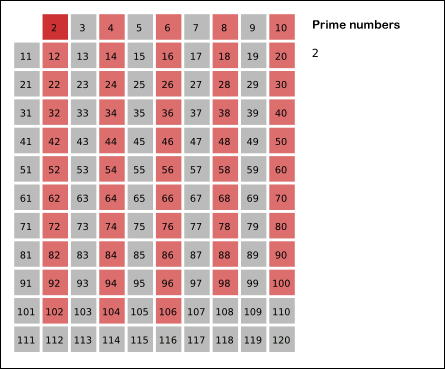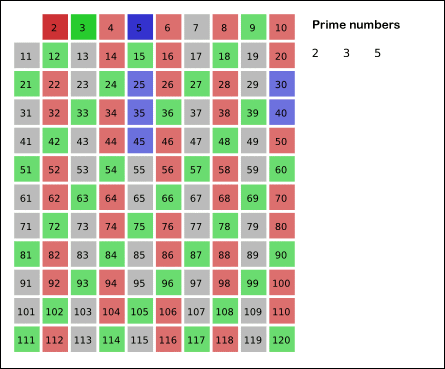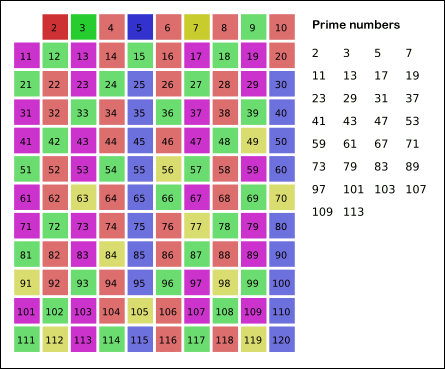
- 6의 경우 2의 배수를 지울 때 지워졌으므로, 남아있는 수 중 7의 배수(특정 수의 배수)를 반복해서 모두 지운다. (이때 특정 수인 7 자기 자신은 제외한다.)
- 특정 수를 제외한 모든 배수가 지워질 때 까지 이를 반복하면, 최종적으로 소수만이 남는다.
에라토스테네스의 체 구현하기
알고리즘을 구현하기 전에 반복 작업을 줄여주기 위한
다음의 정리에 관해서 먼저 알아보고자 한다.
3개 이상의 소수로 구성된 합성수는 그 수의 제곱근보다 작거나 같은 약수를 갖는다.
위의 정리는 아래와 같이 증명할 수 있다.
- $n$을 합성수(*1과 자기 자신 이외의 약수로 이루어진 수)라고 한다.
( ∴ $n = ab$ , $1 < a, b < n$ ) - $a, b$가 “둘 다” $\sqrt{n}$보다 크다고 가정해보자. ( ∴ $a, b > \sqrt{n}$ )
- 이때, $a*b > \sqrt{n} * \sqrt{n}$ → $( ab > n ) ≠ ( ab = n )$ 이 되므로 위의 가정은 모순된다.
- 따라서, 귀류법에 의해서 “$a, b$ 중 하나는 $\sqrt{n}$ 보다 작다”.
위의 정리는 2 ~ $n$ 사이의 숫자 배열에서 소수를 색인하는데 걸리는 반복을 감소시킬 수 있다.
- 2 ~ $n$ 사이에 소수가 아닌 양의 정수 $p$ 와 $q$가 있으며 $p < q$ 를 만족한다.
- 이때, $q$의 약수는 $p$의 약수보다 크거나 같기 때문에
- 2 ~ $n$ 사이의 배열안의 숫자가 가지는 모든 약수 중 가장 큰 약수는 $\sqrt{n}$보다 작을 것이다.
- 따라서, 이를 이용하면 에라토스테네스 알고리즘에서 배수를 지우는 과정이 $\sqrt{n}$회 이하로 줄일 수 있다.
이를 이용해 알고리즘을 파이썬 함수로 구현하면 다음과 같다.
def prime_list(n):
# 총 n개의 요소를 가진 배열 생성(모든 배열의 원소를 소수(TRUE)라고 간주한다.)
sieve = [True]*n
# 위에서 언급한 정의 이용
m = int(n ** 0.5)
for i in range(2, m + 1):
# i가 소수인 경우 / 2(첫 번째 특정 수)부터 먼저 들어온다.
if sieve[i] == True:
# 리스트의 인덱스가 특정 수 i의 배수와 동일할 경우
# 해당 인덱스의 값을 False로 변환한다.
# 2의 경우, sieve[2], sieve[4], ...의 값들을 False로 변환한다.
for j in range(i+i, n, i):
sieve[j] = False
# 소수 목록 산출
# 리스트의 인덱스 값이 True에 해당하는 인덱스 번호만 리스트로 반환
return [i for i range(2, n) if sieve[i] == True]
