[Statistics] 카이제곱검정

in Data on Statistical Analysis


Contents

본 포스팅은 카이제곱검정에 관하여 정리하였습니다.


카이제곱 검정이란?

카이제곱검정(chi-squared test)(혹은 교차분석)은 가설 검정의 관계 검정 분석 기법의 하나이다. 해당 기법은 카이제곱분포에 기초한 통계적인 방법으로, 분포의 기대값과 실제 관측 값이 얼마나 다른지에 관한 여부를 확인하는데 사용되는 검정 기법이다. 종속, 독립 변수 모두 정량적인 수치로 표시할 수 없으며 순서가 없는 명목척도일 때 사용된다.

카이제곱검정은 다시 적합도검정, 동질성 검정, 그리고 독립성 검정으로 나누어진다.

  • 적합도검정 : 범주형 변수가 기대하는 분포를 따르는지에 관한 여부를 검정한다. 실제로 관측된 값과 기대되는 값을 비교하는 검정이다.
  • 동질성 검정 : 사전에 집단을 두 그룹으로 쪼개어 집단간 분포의 동질성을 통해 두 집단 간 차이를 검정한다. 예를 들자면, AB테스트가 있다.
  • 독립성 검정 : 변수들 간의 독립성 또는 관련성(혹은 연관성)을 검증한다. 동질성 검정과 같이 사전에 미리 집단 분리를 하기 어려울 경우에 주로 사용한다. 예를 들자면, 폐암과 담배의 연관성을 알기 위해서 하나의 집단에는 비흡연 그룹, 다른 집단은 흡연 그룹 이렇게 나눌 수 없기 때문에, 폐암이 있는 사람들을 기준으로 담배를 폈는지 혹은 안폈는지 역추적하여 폐암과 흡연의 관계를 알고자 할 때 사용한다.


1-1) 카이제곱분포

먼저, 카이제곱검정에 관하여 알기전에 카이제곱분포에 관하여 알아둘 필요가 있다. 카이제곱분포란 서로 독립적인 표준정규분포의 확률변수를 각각 제곱한 다음 합해서 얻어지는 값이다. 확률변수를 제곱하였기 때문에 0 보다 작은 값은 존재하지 않으며 항상 양수이다.

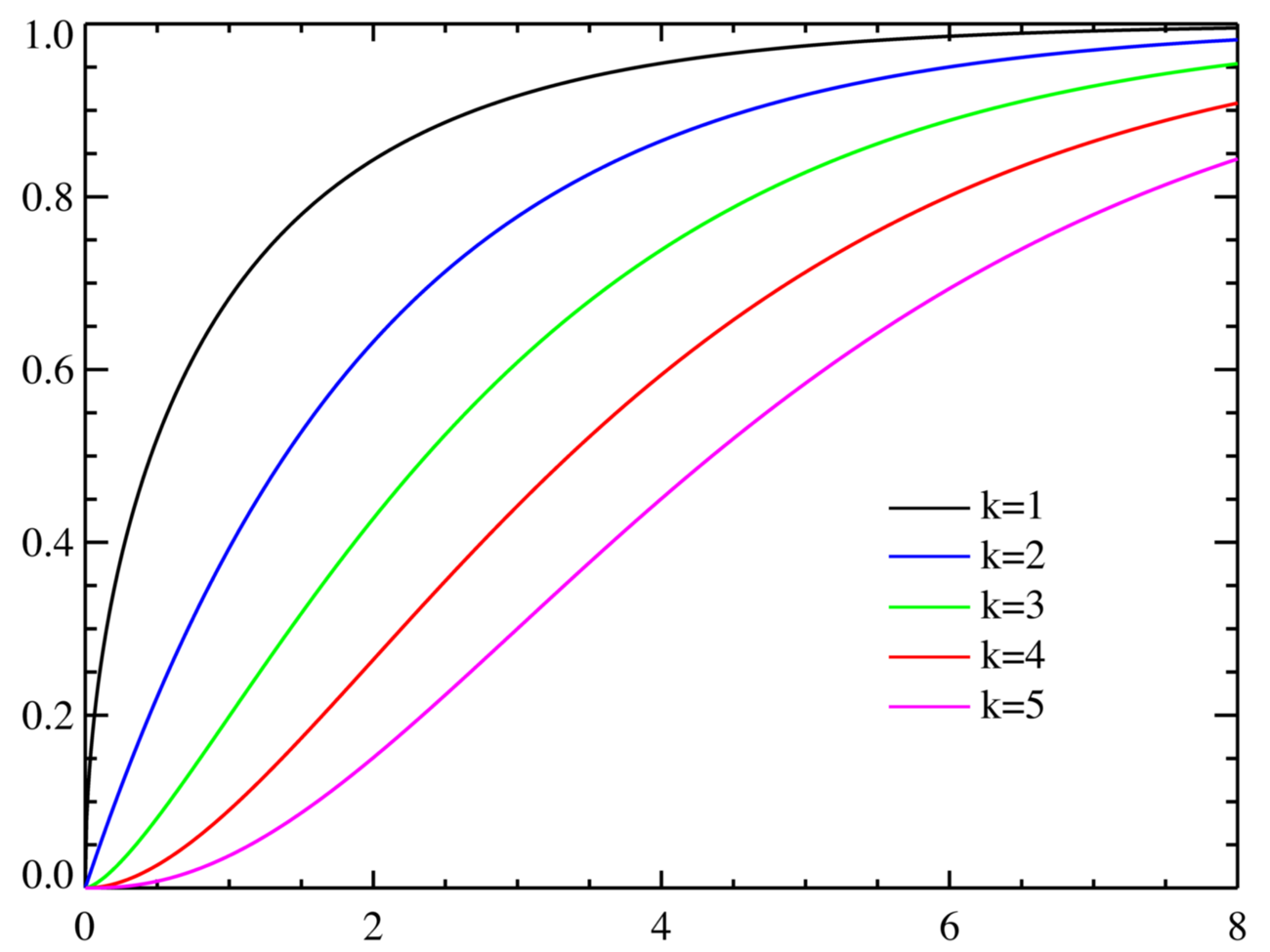
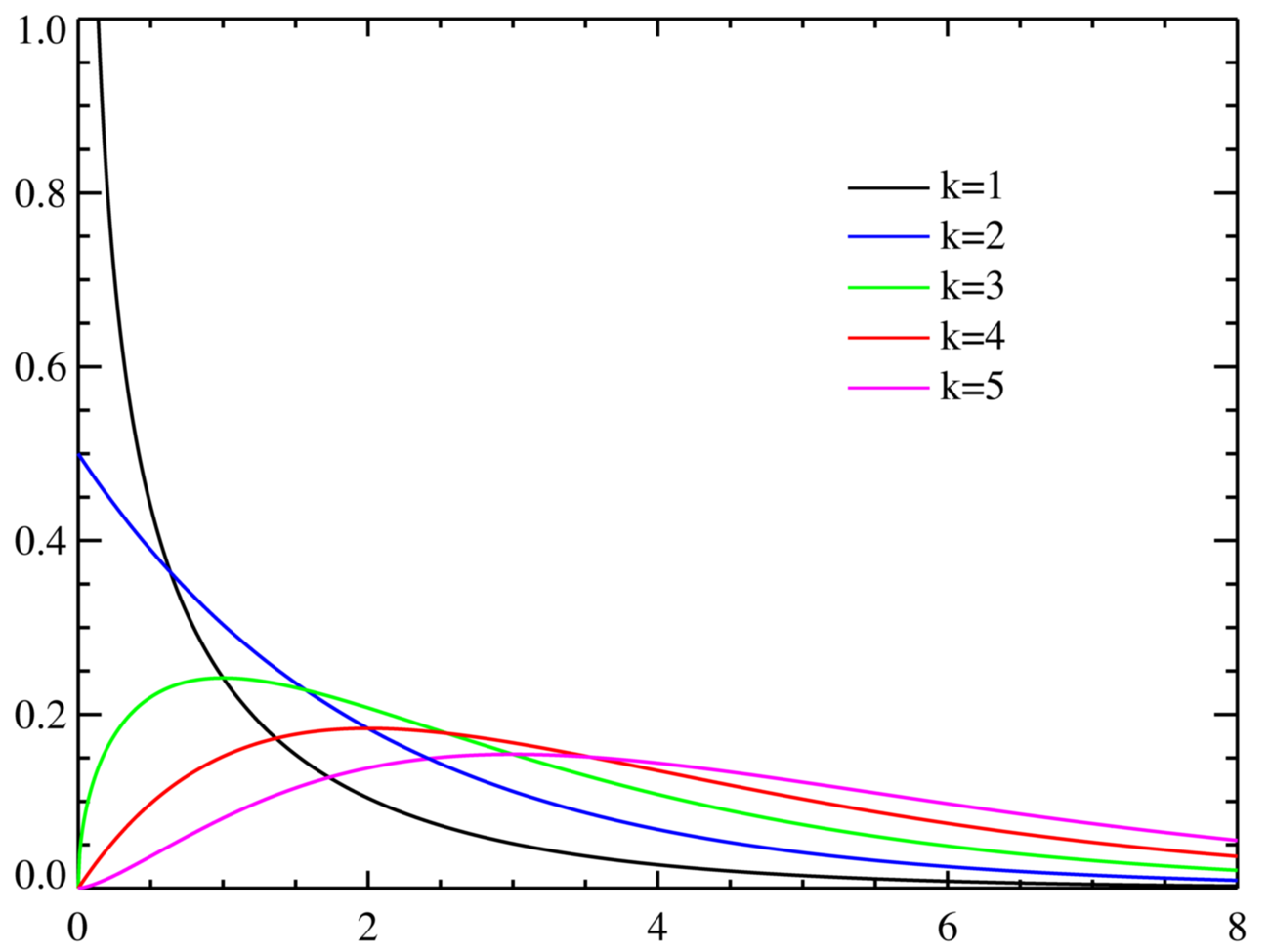
카이제곱분포는 치우침을 대표하는 지표인 분산의 특징을 확률 분포로 나타내었기 때문에, 아래의 사진과 같이 정규분포와 달리 한쪽으로 치우쳐 있다. 하지만, 이러한 분포 모양은 표본의 수에 따라서 달라지기도 한다. 표본의 수가 적을 때에는 치우치는 모양이 되지만, 표본의 수가 많아지면 정규분포와 비슷한 형태로 변형된다. 이는 자유도(defree of freedom)에 의해서도 변형될 수 있다.

카이제곱분포에서 자유도란 제곱하여 합할 때 사용되는 서로 독립적인 표준정규분포의 개수이다. 자유도 n이 작을수록 0 주변에 데이터가 치우치는 비대칭 모양을 형성하며, 자유도 n이 클수록 카이제곱분포는 정규분포에 근사하게된다.

context

context


1-2) 카이제곱분포 표현식

자유도 k의 카이제곱 분포는 표준정규분포를 따르는 k개의 독립적인 확률변수

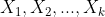
CodeCogsEqn

가 있을 때, 이 확률변수들을 각각 제곱해서 다음과 같이 합한 값이다.

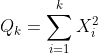
CodeCogsEqn_(8)

이에 따른, 자유도별 카이제곱분포는 다음과 같다.

  • k=1

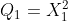
CodeCogsEqn_(5)

  • k=2

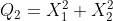
CodeCogsEqn_(6)

  • k=3

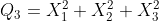
CodeCogsEqn_(7)

더불어, 카이제곱분포를 따르는 확률분포라고 표시할 때는 다음과 같이 표시한다.

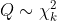
CodeCogsEqn_(4)


카이제곱 통계량

카이제곱 통계량은 데이터의 분포에서 실제 관측값(O_i)와 가정된 분포의 기댓값(E_i)의 차이나타내는 측정값이다. 이러한 관측값과 기댓값의 차이를 나타내기위해서 카이제곱분포를 이용하는 것이고 수식은 아래와 같다. 여기서 분자를 기대값으로 다시 나눠주는 이유는 상대적 차이를 반영하기 위함이다. 예를 들어, 1000이라는 값을 기대하였을 때 1001이 나오는 것과 10을 기대했을 때 9가 나오는 것의 차이를 기대값으로 나누어 가중치를 차별화 시키는 것이다.

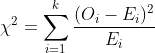
CodeCogsEqn_(9)


카이제곱검정(적합도검정) 예제

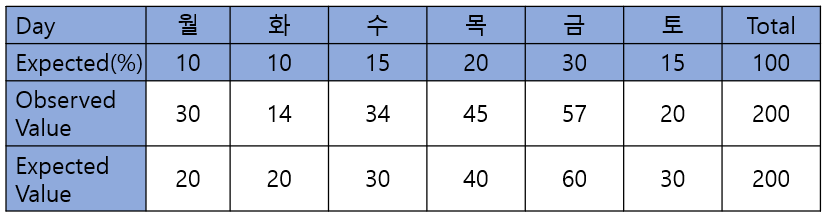
다음과 같이 가게의 주인이 제공해준 1주일 중 월요일에서 토요일 동안 일별 손님이 방문하는 기대 분포(Expected(%))와 실제 관측된 값(Observed Value)이 있다. 이때, 가게의 주인이 준 분포가 맞는지 카이제곱검정(적합도검정)을 통해 확인해보자.

귀무가설은 “가게의 주인이 전달해준 손님 방문 기대 분포가 맞다”가 될 것이며, 대립가설은 “가게의 주인이 전달해준 손님 방문 기대 분포는 틀리다”가 될 것이다. 그리고, 주인이 준 분포가 참이라고 가정했을 때, 기대 관측 값(Expected Value)는 실제 관측된 값의 전체 합(200)을 기대 분포별로 계산한 값이 될 것이다. (*유의수준은 5%를 사용하자)

Untitled 1


이를 이용하여, 다음과 같이 11.44라는 카이제곱 통계치를 계산할 수 있다.

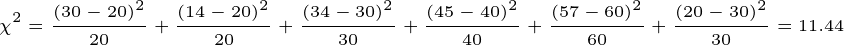
CodeCogsEqn_(13)


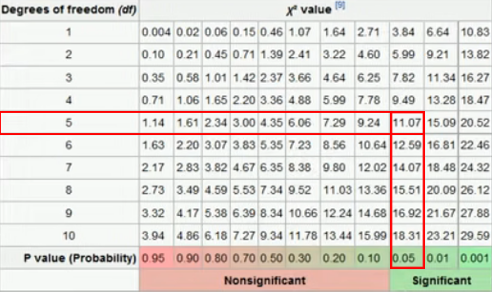
다음으로, 유의수준(p-value)와 자유도를 이용하여 임계점의 카이제곱값을 카이제곱분포표를 통해서 찾아낼 수 있다. 자유도의 경우 월, 화, 수, 목, 금, 토라는 총 6개의 범주를 사용하기에 6의 값을 가질 것 같지만 6에서 1을 뺀 값인 5이다. 왜냐하면, 범주의 크기가 n인 표본의 관측값에서 n-1개를 먼저 선별하면 나머지 1개의 값이 정해지기 때문이다. 따라서, (df = 5, p = 0.05)의 카이제곱값을 분포표에서 찾게되면 11.07이라는 것을 확인할 수 있다. 즉, 적어도 11.07이상의 카이제곱 극값을 얻을 확률이 5%라는 의미이다.

Untitled 2


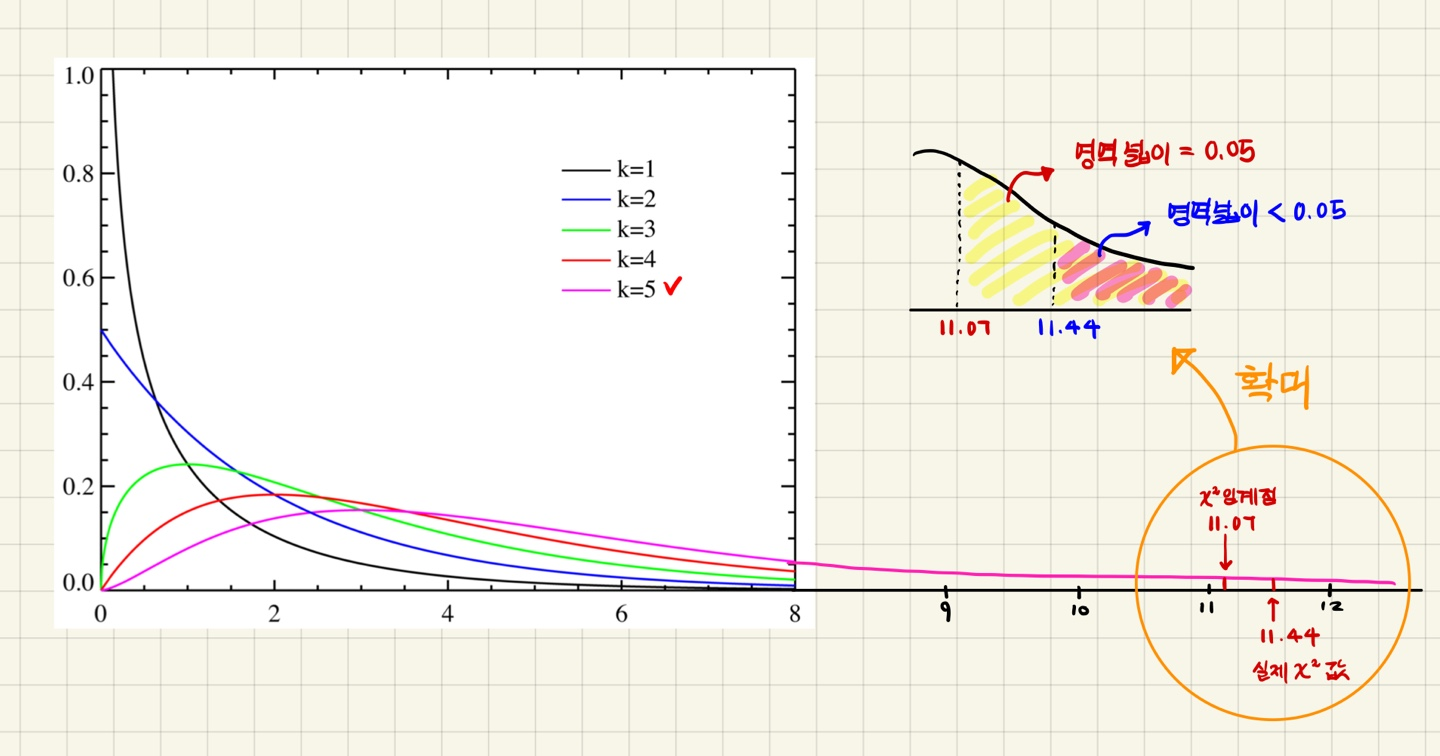
마지막으로, k=5인 카이제곱 분포(핑크색선)을 기준으로 실제로 구한 카이제곱값(11.44)는 임계점의 카이제곱값(11.07)보다 수치적으로 커보일 수 있지만, 카이제곱값으로 부터 집계되는 유의수준에 초점을 맞추어야한다. 영역의 넓이를 통해 유의수준(5%) 보다 작은 것을 확인할 수 있다. 따라서, 귀무가설은 기각되어졌기 때문에 가게의 주인이 준 분포표는 실제가 아님을 확인하였다.

Untitled 3


References